转速与角速度转换公式详解
转速和角速度的转换公式是机械工程中常用的基础知识,尤其在涉及旋转机械和动力学分析时显得尤为重要。在许多实际工程应用中,了解转速和角速度之间的转换关系对于设计和分析旋转系统至关重要。转速通常描述为每分钟旋转的圈数(RPM),而角速度则通常以弧度每秒(rad/s)来表示。本文将详细探讨转速和角速度的基本概念、转换公式及其应用。

转速(Revolution Per Minute,RPM)是衡量旋转物体每分钟旋转圈数的物理量。在日常生活和工程应用中,RPM是一个非常直观的参数,可以很容易地通过旋转物体的视觉观察或使用转速表进行测量。例如,在汽车发动机中,我们常常听到“这台发动机的最大转速为7000 RPM”这样的描述,它表示发动机每分钟可以旋转7000圈。

角速度(Angular Velocity)则是描述旋转物体单位时间内角度变化的物理量,通常用ω表示,单位是弧度每秒(rad/s)。角速度是一个矢量量,既有大小又有方向,其方向垂直于旋转平面,遵循右手螺旋定则。在物理学和工程学中,角速度提供了旋转物体动态行为的重要信息,如旋转加速度、旋转动能等。
转速和角速度之间的转换公式是基于两者定义的基本关系推导出的。具体来说,转速与角速度之间的转换关系可以表示为:
ω = (2π × RPM) / 60
其中,ω是角速度,单位是弧度每秒(rad/s);RPM是转速,单位是每分钟旋转的圈数。这个公式的推导基于以下事实:一分钟有60秒,而一圈(360度)等于2π弧度。因此,将RPM乘以2π,得到每分钟的角度变化量(以弧度为单位),然后再除以60,即可得到每秒的角度变化量,即角速度。
反之,从角速度转换为转速的公式为:
RPM = (60 × ω) / (2π)
这个公式的推导是上面公式的逆过程,它允许我们从角速度计算出转速。
了解这些转换公式后,我们可以通过具体实例来加深理解。假设一个旋转物体的转速为3000 RPM,我们需要计算其角速度。应用转换公式:
ω = (2π × 3000) / 60
= (2π × 50)
≈ 314.16 rad/s
同样,如果给定一个旋转物体的角速度为100 rad/s,我们可以计算其转速:
RPM = (60 × 100) / (2π)
≈ (6000 / 6.2832)
≈ 954.93 RPM
转速和角速度转换公式的应用广泛存在于各种机械工程和物理学领域。例如,在航空航天工程中,了解卫星和飞行器的旋转部件的角速度对于姿态控制和稳定性分析至关重要。在汽车工程中,发动机的转速和角速度对于燃油效率、动力输出和发动机寿命具有重要影响。在机械设计中,轴、轴承和齿轮的转速和角速度特性决定了系统的性能和可靠性。
此外,转速和角速度的转换公式在动力学分析中也扮演着重要角色。动力学研究物体在力的作用下如何运动,而旋转物体的运动分析往往涉及转速和角速度的计算。例如,在刚体动力学中,了解物体的角速度和角加速度可以帮助我们计算其动能、动量和角动量,从而分析物体的动态行为。
值得注意的是,虽然转速和角速度在概念上有所不同,但在实际应用中,它们往往相互关联。在旋转系统中,转速的变化通常伴随着角速度的变化,反之亦然。因此,在进行旋转系统的设计和分析时,我们需要综合考虑转速和角速度的影响。
此外,还有一些特殊情况需要注意。例如,在旋转系统的启动和停止过程中,转速和角速度的变化往往是非线性的,这可能导致系统的动态行为变得更加复杂。因此,在进行旋转系统的动态分析时,我们需要考虑这些非线性因素的影响。
总的来说,转速和角速度的转换公式是机械工程中不可或缺的基础知识。通过掌握这些转换公式,我们可以更好地理解和分析旋转系统的行为,从而优化系统的设计和性能。无论是航空航天、汽车工程还是机械设计领域,转速和角速度的概念和转换公式都发挥着重要作用。
此外,随着技术的不断进步和工程领域的不断拓展,转速和角速度的测量和分析方法也在不断更新和改进。例如,现代传感器技术和数据采集系统可以实时监测旋转物体的转速和角速度,为工程师提供准确的数据支持。同时,计算机仿真和建模技术也为我们提供了强大的工具,用于预测和分析旋转系统的行为。
因此,作为工程师和科研人员,我们需要不断学习和掌握新的技术和方法,以更好地应对日益复杂的工程挑战。同时,我们也需要保持对基础知识的学习和掌握,因为正是这些基础知识构成了我们理解和分析复杂系统的基石。转速和角速度的转换公式正是这样一组基础知识,它们在我们理解和分析旋转系统的过程中发挥着不可替代的作用。
综上所述,转速和角速度的转换公式是机械工程中不可或缺的
- 上一篇: 如何让新买的耳机达到最佳音效?煲机秘籍大公开!
- 下一篇: 2023年邮政快递收费标准表是怎样的?
-
 转速与角速度:轻松掌握转换公式资讯攻略11-05
转速与角速度:轻松掌握转换公式资讯攻略11-05 -
 揭秘:灵敏度计算公式详解资讯攻略11-03
揭秘:灵敏度计算公式详解资讯攻略11-03 -
 角度制与弧度制相互转换的公式是什么资讯攻略10-29
角度制与弧度制相互转换的公式是什么资讯攻略10-29 -
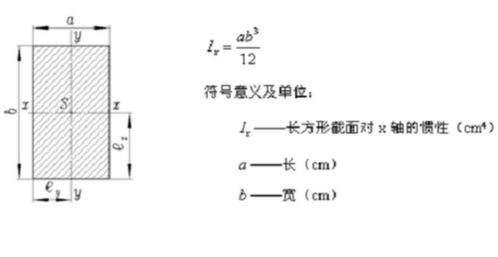 揭秘:惯性矩的精准计算公式大公开!资讯攻略11-15
揭秘:惯性矩的精准计算公式大公开!资讯攻略11-15 -
 是否需要将笔记本硬盘从5400转升级至7200转?资讯攻略11-21
是否需要将笔记本硬盘从5400转升级至7200转?资讯攻略11-21 -
 角度与弧度轻松转换秘籍资讯攻略11-25
角度与弧度轻松转换秘籍资讯攻略11-25