角度制与弧度制相互转换的公式是什么

在数学领域中，角度制和弧度制是两种描述角的大小的不同方式。尽管它们在表现形式上有所不同，但通过特定的转换公式，可以在这两种制度之间进行无缝转换。角度制，顾名思义，是以“度”作为基本单位来衡量角的大小，广泛应用于日常生活和初等数学教育中。与之相对的弧度制，则是以弧长与半径的比值来描述角，这一制度在高等数学和物理学中更为常见。

首先，我们来深入了解角度制。角度制起源于古代天文学和地理学，由于人类对于日月星辰运行轨迹的观察，以及地图制作的需要，逐渐形成了角度的概念。在角度制中，一个完整的圆被划分为360度，一个直角等于90度，一个平角等于180度，而一个周角，即一个完整的圆，则等于360度。这种划分方式简单直观，便于理解和计算，因此在日常生活中得到了广泛应用。

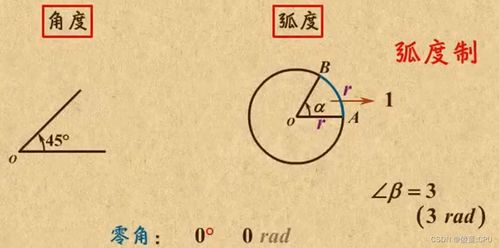
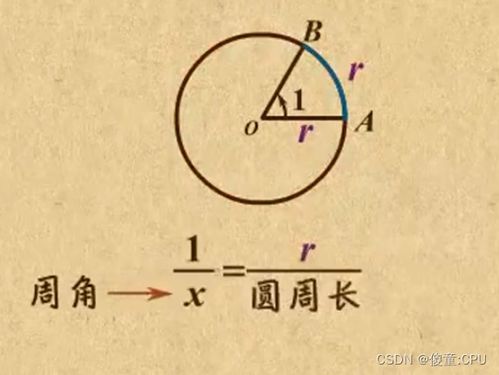
然而，随着数学和物理学的深入发展，人们发现角度制在进行某些计算时存在不便。例如，在计算三角函数值时，角度制需要引入复杂的单位换算和周期性质，而弧度制则能更加简洁地表达这些关系。弧度制的基本思想是，以圆的半径为长度，在圆上截取一段弧，这段弧所对应的圆心角的大小，就定义为这段弧长与半径的比值。在这个定义下，一个完整的圆所对应的圆心角大小就是2π，因为圆的周长是2πr，而弧长与半径的比值正是2π。

接下来，我们重点讨论角度制和弧度制之间的转换公式。这些公式是连接两种制度的桥梁，使得我们可以根据需要在它们之间进行自由转换。

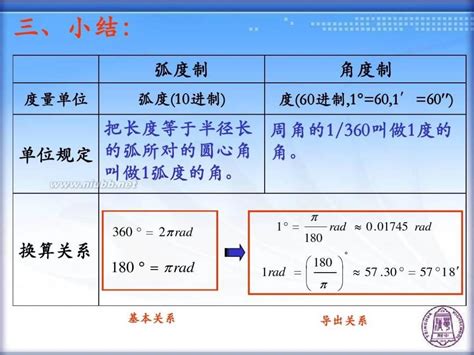
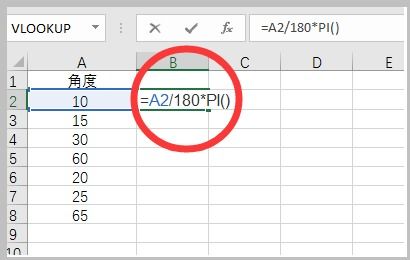
第一个转换公式是将角度制转换为弧度制。这个公式的形式是：弧度 = 度数 × (π/180)。这里的π是一个无理数，约等于3.14159，它是圆周率，表示圆的周长与直径的比值。180则是角度制中一个完整圆所对应的度数。通过这个公式，我们可以轻松地将任何角度制的度数转换为弧度制。例如，要将90度转换为弧度制，我们只需将90乘以π/180，得到π/2弧度。

第二个转换公式是将弧度制转换为角度制。这个公式的形式是：度数 = 弧度 × (180/π)。与第一个公式相反，这个公式将弧度值转换为角度值。同样地，这里的π和180分别代表圆周率和角度制中一个完整圆所对应的度数。通过这个公式，我们可以将任何弧度制的值转换为角度制。例如，要将π/4弧度转换为角度制，我们只需将π/4乘以180/π，得到45度。

这两个转换公式不仅在数学计算中发挥着重要作用，还在物理学、工程学等领域中得到了广泛应用。在物理学中，很多物理现象和规律都与角度有关，而弧度制在描述这些现象和规律时更加简洁和直观。在工程学中，角度制和弧度制也经常被用于描述物体的旋转角度和位置关系。通过掌握这两个转换公式，我们可以更加灵活地在不同领域中使用角度制和弧度制。

此外，角度制和弧度制之间的转换还有助于我们深入理解三角函数。三角函数是一类重要的数学函数，包括正弦函数、余弦函数、正切函数等。这些函数在角度制和弧度制下有着不同的表现形式和性质。例如，在角度制下，正弦函数的周期为360度或2π弧度（在弧度制下），而在弧度制下，正弦函数的周期则直接表示为2π。通过对比和分析这两种制度下的三角函数性质，我们可以更加深入地理解三角函数的本质和特征。

值得一提的是，角度制和弧度制之间的转换并不仅仅是数学上的技巧或工具，它们还反映了人类对于自然界和数学世界的不同理解和描述方式。角度制更侧重于直观性和实用性，而弧度制则更强调逻辑性和简洁性。这两种制度各有优劣，但它们之间的转换却为我们提供了一个更加全面和深入的视角来审视和理解数学世界。

总之，角度制和弧度制是描述角的大小的两种不同方式。通过掌握它们之间的转换公式，我们可以更加灵活地在不同领域中使用这两种制度，并在数学学习和研究中取得更好的效果。同时，这两种制度也为我们提供了一个更加全面和深入的视角来审视和理解数学世界以及与之相关的物理学和工程学等领域。在未来的学习和研究中，我们应该继续深入探索和理解这两种制度及其相互关系，以更好地应用它们来解决实际问题并推动科学和技术的发展。