如何将弧度转换为角度?
在数学和物理学中,角度和弧度是描述旋转或圆周运动的两种基本单位。尽管它们各自有其应用场景,但在很多情况下,我们需要在弧度与角度之间进行转换。本文旨在详细介绍如何将弧度换算成角度,帮助读者更好地理解这两种度量单位之间的关系。
一、弧度与角度的基本概念
1.1 角度
角度是我们日常生活中经常使用的度量单位,通常用于描述两条射线与其共同的端点之间的夹角。角度的单位有度(°)、分(′)和秒(″),其中1度等于60分,1分等于60秒。在平面几何中,一个完整的圆周角等于360度。
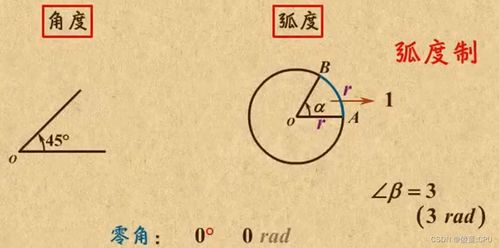
1.2 弧度
弧度则是另一种度量旋转或圆周运动的方式,它是基于圆的半径来定义的。具体来说,一个圆的周长与半径的比值(即2π)被定义为弧度制下的一个完整圆周角,也就是360度所对应的弧度值。因此,在弧度制中,一个完整的圆周角等于2π弧度。

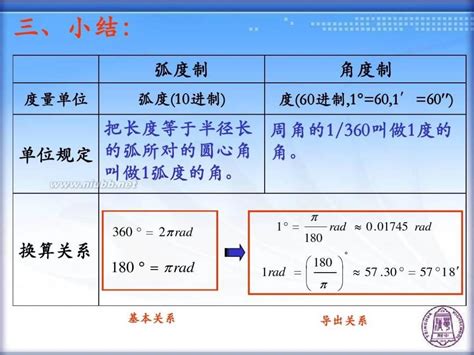
二、弧度与角度之间的换算关系
为了将弧度换算成角度,我们需要知道弧度与角度之间的基本换算公式。这个公式如下:
\[ \text{角度} = \text{弧度} \times \frac{180}{\pi} \]
或者,如果我们想要将角度换算成弧度,可以使用以下公式:
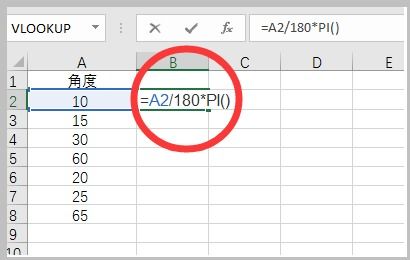
\[ \text{弧度} = \text{角度} \times \frac{\pi}{180} \]
这两个公式为我们提供了在弧度与角度之间进行转换的数学基础。
三、弧度换算成角度的详细步骤
3.1 确定弧度值
首先,我们需要知道要转换的弧度值是多少。这个值可能是通过计算得到的,也可能是题目直接给出的。
3.2 应用换算公式
接下来,我们将这个弧度值代入到换算公式中。公式是:
\[ \text{角度} = \text{弧度} \times \frac{180}{\pi} \]
这里需要注意的是,π是一个无理数,其值大约为3.14159。在实际计算中,我们可以使用计算器或查表来得到π的近似值。
3.3 进行计算
将弧度值代入公式后,我们就可以进行计算了。这个计算过程通常涉及乘法和除法运算。
3.4 得出结果
最后,我们将计算得到的结果四舍五入到合适的位数(根据需要),并注明单位是度。
四、实际应用案例
为了更好地理解如何将弧度换算成角度,我们来看几个实际的应用案例。
4.1 案例一:简单换算
假设我们有一个弧度值为π/4的角,我们需要将其换算成角度。
\[ \text{角度} = \frac{\pi}{4} \times \frac{180}{\pi} = \frac{180}{4} = 45^\circ \]
因此,π/4弧度等于45度。
4.2 案例二:三角函数中的换算
在三角函数中,角度和弧度是两种常用的自变量单位。例如,在正弦函数sin(x)中,x可以表示角度也可以表示弧度。如果我们知道一个角的正弦值,并且这个角是用弧度表示的,但我们想要知道这个角对应的角度值是多少,那么我们就需要进行弧度到角度的换算。
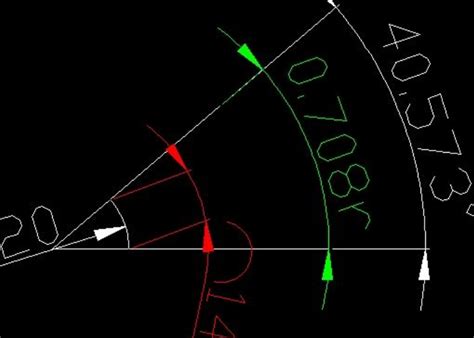
假设sin(x) = 0.7071,且x是用弧度表示的。我们知道,当角度为45度时,正弦值为0.7071(在近似情况下)。但是,为了验证这一点,我们可以将x换算成角度。
首先,我们需要找到满足sin(x) = 0.7071的x值(在弧度制下)。通过查表或使用计算器,我们可以得到x ≈ π/4(在近似情况下)。
然后,我们将这个弧度值换算成角度:
\[ \text{角度} = \frac{\pi}{4} \times \frac{180}{\pi} = 45^\circ \]
因此,我们验证了当sin(x) = 0.7071时,x对应的角度值为45度。
4.3 案例三:物理学中的应用
在物理学中,弧度与角度之间的换算也是非常重要的。例如,在圆周运动或摆动问题中,我们可能需要知道某个角度对应的弧度值是多少,以便进行进一步的计算和分析。
假设一个单摆的摆动角度为30度,我们需要计算这个角度对应的弧度值。但是,在这个案例中,我们实际上是要进行角度到弧度的换算(尽管题目要求的是弧度换算成角度的说明文章,但这个反向过程也有助于理解两者之间的转换)。
\[ \text{弧度} = 30^\circ \times \frac{\pi}{180} = \frac{\pi}{6} \]
虽然这个案例是角度到弧度的换算,但它同样展示了如何在实际问题中应用换算公式。
五、总结
通过将弧度换算成角度,我们可以更好地理解这两种度量单位之间的关系,并在需要时进行相互转换。本文详细介绍了弧度与角度的基本概念、换算关系以及换算步骤,并通过实际应用案例来加深理解。希望读者在阅读本文后能够熟练掌握弧度与角度之间的换算方法,并在实际问题中灵活运用。无论是在数学、物理学还是其他相关领域,这种换算能力都是非常重要的。
- 上一篇: 现货农产品有哪些常见问题?
- 下一篇: 手机百度钱包无手续费转账教程
-
 Win10计算器中将角度转换为弧度的方法资讯攻略11-09
Win10计算器中将角度转换为弧度的方法资讯攻略11-09 -
 角度制和弧度制之间如何转换?资讯攻略11-09
角度制和弧度制之间如何转换?资讯攻略11-09 -
 角度与弧度轻松转换秘籍资讯攻略11-25
角度与弧度轻松转换秘籍资讯攻略11-25 -
 角度制与弧度制相互转换的公式是什么资讯攻略10-29
角度制与弧度制相互转换的公式是什么资讯攻略10-29 -
 揭秘:1度与弧度之间的神秘换算关系资讯攻略01-09
揭秘:1度与弧度之间的神秘换算关系资讯攻略01-09 -
 轻松掌握:弧度与角度的换算方法资讯攻略11-15
轻松掌握:弧度与角度的换算方法资讯攻略11-15









