如何根据三角形三边长计算面积

在几何学中，三角形是最基本也是最重要的形状之一。了解三角形的面积计算方法，不仅能帮助我们解决日常生活中的实际问题，还能深化对数学原理的理解。三角形面积的计算方法多样，依据已知条件的不同，可以选择最合适的方法。本文将从三角形的边长、高度、角度以及海伦公式等多个维度，详细探讨如何计算三角形的面积。

边长与高度

最直观的三角形面积计算方法是基于底边和高度的公式。设三角形的底边长为b，高度为h，则三角形的面积A可以通过以下公式求得：

A = 0.5 × b × h

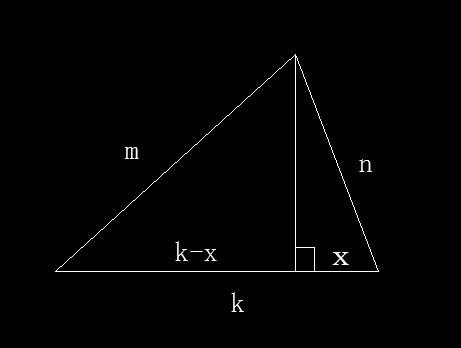
这个公式简单明了，但在实际应用中，有时底边和高度的具体数值并不容易直接获取。例如，在面对一个不规则形状的三角形区域时，直接测量底边和高度可能相当困难。此时，我们可能需要借助其他边长或角度信息，通过几何关系来间接求出底边或高度。

使用两条边和夹角

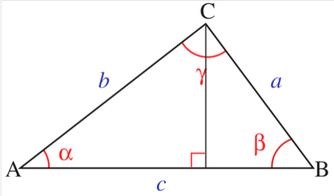
如果我们知道三角形中的两条边长以及它们之间的夹角，那么可以利用正弦定理来计算三角形的面积。设三角形的两条边长为a和b，它们之间的夹角为θ（以弧度为单位），则三角形的面积A可以通过以下公式计算：

A = 0.5 × a × b × sin(θ)

这种方法在涉及角度信息时尤为有用。例如，在建筑设计中，我们可能需要根据两栋建筑物之间的距离和它们之间的夹角来计算它们所夹空间的面积，此时正弦定理便派上了用场。

海伦公式

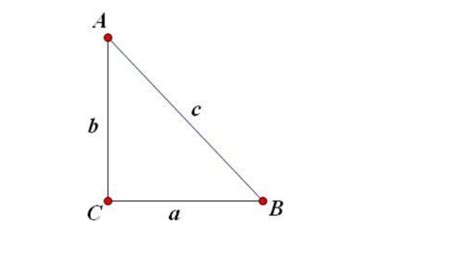
海伦公式是一种非常通用的三角形面积计算方法，它仅依赖于三角形的三边长，而不涉及高度或角度。设三角形的三边长分别为a、b和c，首先计算半周长s：

s = 0.5 × (a + b + c)

然后，利用海伦公式计算面积A：

A = √(s × (s - a) × (s - b) × (s - c))

海伦公式的推导涉及到复杂的几何和代数运算，但其应用却异常简便。这一公式在处理只知道三角形三边长而不知道高度或角度的问题时尤为有效，例如，在地质勘探中，我们可能需要根据地面三个点的相对距离来计算它们围成的三角形区域的面积。

直角三角形的特殊情况

对于直角三角形，面积的计算更为简单直接。设直角三角形的两条直角边分别为a和b，则面积A可以直接通过以下公式求得：

A = 0.5 × a × b

直角三角形的面积计算之所以简单，是因为其高度（即直角边之一）与底边（另一条直角边）垂直，无需通过复杂的几何变换来求解。这一特性使得直角三角形在面积计算中具有独特的优势。

向量方法

在高等数学中，我们还可以利用向量的叉积来计算三角形的面积。设三角形的三个顶点分别为A、B和C，对应的向量分别为→AB和→AC。则三角形的面积A可以通过以下公式计算：

A = 0.5 × |→AB × →AC|

这里的“×”表示向量的叉积运算，其结果是一个向量，其模等于原两个向量构成的平行四边形的面积，方向垂直于这两个向量所构成的平面。对于三角形而言，其面积即为该平行四边形面积的一半。向量方法不仅简洁优雅，而且具有广泛的适用性，它不仅能够处理平面三角形，还能扩展到三维空间中的多面体面积计算。

几何变换与面积守恒

在某些复杂情况下，我们可能需要对三角形进行几何变换，如平移、旋转或缩放，以简化面积计算。值得注意的是，在平移和旋转过程中，三角形的面积保持不变；而在缩放过程中，面积会按照缩放比例的平方进行变化。因此，在利用几何变换简化面积计算时，需要特别注意面积守恒的原理。

数值方法与近似计算

在实际应用中，有时我们可能无法精确测量三角形的边长或角度，或者需要处理的三角形形状过于复杂，以至于无法直接应用上述公式进行计算。此时，我们可以考虑采用数值方法或近似计算来求解三角形的面积。例如，可以利用数值积分的方法来计算由曲线围成的三角形区域的面积；或者，在精度要求不高的情况下，可以通过对三角形进行分割和近似，将其转化为一系列小矩形或梯形的面积之和。

结语

综上所述，三角形面积的计算方法多种多样，每一种方法都有其独特的适用场景和优势。在实际应用中，我们应根据具体问题的特点，选择最合适的方法进行计算。同时，通过学习和掌握这些不同的计算方法，我们可以更深入地理解三角形的几何特性，提高解决实际问题的能力。无论是在日常生活、工程设计还是科学研究中，三角形面积的计算都扮演着不可或缺的角色，它不仅是数学原理的生动体现，更是解决实际问题的重要工具。